Lockdowns of Young People Lead to More Deaths from Covid-19

Covid-19 has given scientific models a bad name. The predictions from these models have been horribly wrong. The problem was not with modelling; rather the problem was with poor choices of model parameters. One can get any mortality result ranging from none to 100% depending on the choices made for model parameters. Garbage in leads to garbage out.
Rather than equating garbage out predictions with “science” we should use scientific data to develop useful models of the mechanisms of virus transmission.
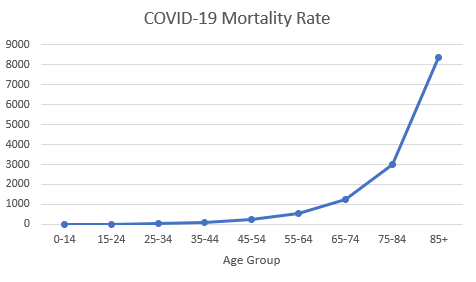
Age Matters
Figure 1 illustrates why case counts are poor predictors of mortality. Case counts can only predict mortality if the age composition of the people tested remains constant over time. Monitoring case counts following policy changes that affect young people will have little or no predictive value for mortality. If we want to understand mortality, we are stuck with monitoring mortality.
Sweden: Voluntary Restriction Rather Than Lockdown
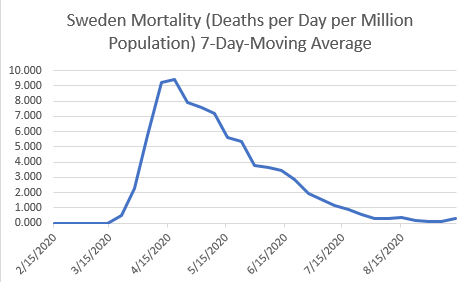
Contrary to what some have published, Sweden did not “let it rip.” It banned gatherings of more than 50 people for some time. Otherwise, Sweden advised people to social distance and use masks, but it did not have any mandatory restrictions. Sweden did not close its schools or its bars. Sweden advised older people to exercise greater caution, but it left individual decisions to the individuals affected by those decisions.
Further, the results in Sweden were not a catastrophe. As of October 10, the total mortality from Covid-19 was 583 deaths per million population. This mortality rate compares favorably to countries that utilized indiscriminate lockdowns including USA (660), Spain (704), UK (628), Italy (597), and Belgium (875). Sweden provides a control group by which we can understand the dynamics of Covid-19 mortality.
Engineers will immediately see the similarity between Figure 1 and the impulse response of a capacitor discharging to ground through a resistance or a water reservoir discharging water through a pipe to homes at sea level. The dynamics of such networks are described by first order linear differential equations that can be solved exactly. The solution is an exponential decay from an initial value toward zero over time.
The initial value is determined by the amount of initial charge on the capacitor or the volume of water initially in the reservoir. The exponential rate of decay is determined by a time constant, but the rate of decay is proportional to the amount remaining to decay. For the Covid-19 mortality system, this result would be achieved by the rapid exposure of an initial number of people vulnerable to death followed by a fixed probability of death each day of remaining cases that had neither died nor resolved. We can now consider different types of changes to this system and predict how the system would respond to those changes.
New York: Increasing the Volume of Water in the Reservoir
There are several steps necessary for Covid-19 to result in mortality. A person must be exposed to the virus. An exposed person must become ill by failing to immediately kill the virus. An ill person must die by losing the battle between host defenses and virus replication. Figure 1 shows that exposure of an elderly person is much more likely to result in death than exposure of a young person. What processes are likely to change the peak in the curve illustrated in Figure 2?
Let us consider processes that change transmission of virus from an elderly person to another elderly person. Elderly people are congregated in institutions such as nursing homes. The total number of elderly people can be either divided into many small groups or a few large groups. Small numbers of large groups mean that each entry of virus from outside the group into the group affects a greater number of elderly people.
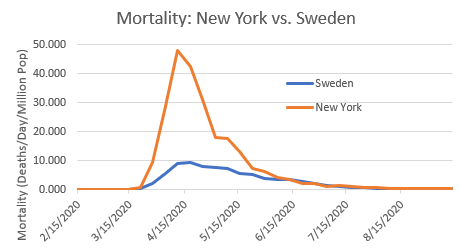
On March 25, 2020 Governor Cuomo ordered that New York nursing homes accept patients from hospitals with positive tests for the Covid-19 virus. The likely intent of this order was to free up hospital beds for new patients with Covid-19, but the unintended consequences of this order are illustrated in Figure 3. Figure 3 shows that, compared to Sweden, New York had a much higher peak, a nearly identical rise time, and a similar pattern of decay from peak toward zero. The nursing home order increased the volume of water in the reservoir or the amount of charge on the capacitor. More elderly nursing home patients were exposed to the virus than would have been exposed otherwise. Once exposed, subsequent lockdowns of young people by closing schools and closing bars had no effect on the mortality curve.
Flattening the Curve
By March of 2020 there were concerns that hospitalizations due to Covid-19 would overwhelm the healthcare system. The stated purpose of indiscriminate lockdowns was to “flatten the curve.” What does “flatten the curve” mean? For a normal distribution, flattening the curve means a larger standard deviation. This produces a lower peak, a larger distance from mean to one standard deviation, and no change in area under the curve. The consequences of “flattening the curve” depend on which types of social interactions are disrupted. One can categorize interactions into three types: interactions among elderly people; interactions among young people; and interactions between young people and elderly people. Closing entry of patients positive for Covid-19 into nursing homes decrease interactions among elderly people with little effect on the other two types of interaction. As seen in the New York example illustrated in Figure 3, minimizing this type of interaction would have favorable results.
Closing elementary schools decrease interactions among young people with little effect on the other two types of interaction. What is the expected result from decreasing this type of interaction? Transmission of virus from the young to the elderly requires transmission of the virus to young people interacting with the elderly. This type of transmission can be reduced by one of two methods: herd immunity, or blocking interactions between young and elderly people.
Indiscriminate lockdowns of young people reduce transmission to those young people who will interact with the elderly, but these lockdowns also delay herd immunity. Rather than an impulse response, we will expect a pulse response with equal area under the pulse and the impulse. The pulse has lower peak amplitude and longer duration.
For simplification of visualization, a pulse can be considered to be short if the mortality curve continues to climb after the pulse stops due to the incubation period. The system response to these short pulses will be similar to the impulse response in shape, but the system response will have a slower rate of climb, a delayed peak, a lower peak amplitude, but an equal area under the curve.
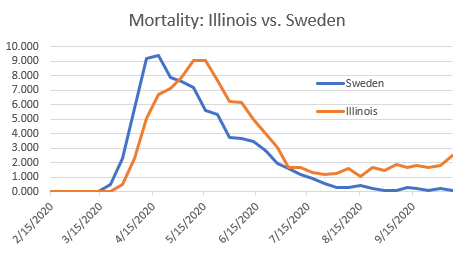
Illinois started an indiscriminate lockdown on March 19, 2020. One can see a slower rate of ascent, a lower peak, and a delayed peak compared to Sweden. As of October 10, the total Covid-19 mortality was 725 per million population in Illinois compared to 583 in Sweden. At best flattening the curve can only achieve equal results to voluntary actions.
Lockdowns of Young Increase Deaths Rather than Prevent Deaths
On April 1, 2020 Dr Anthony Fauci indicated that lockdowns would have to continue until there were zero new cases. This policy indicated a strategy whose goal was eradication of the virus through lockdown. The premise that the virus could be eradicated was a false one. While individual virus particles can certainly be killed, the Covid-19 virus cannot be eradicated. If the virus could be eradicated, then Australia would have already succeeded with its brutal lockdown.
All of the scientific data, as opposed to the wishful thinking coming out of Garbage In Garbage Out models, indicates that the virus is here forever – much like influenza. Given the fact that the virus will eventually spread to the entire young and economically active population, lockdowns of the young cannot possibly achieve reduced mortality compared to voluntary action.
Figure 4 provides a hint as to the explanation. The Sweden curve declined to essentially zero mortality. The Illinois curve did not. The reason is the expected system response to a long pulse. A long pulse is one where the mortality curve has reached a peak and begun to decline before the pulse ends.
The pool of patients who can die from Covid is determined by the balance between two processes. Patients enter the pool by being exposed to virus. Patients leave the pool by case resolution. Once a patient dies or recovers, that patient is no longer at risk for death. There is a natural decline rate proportional to the number of patients in the pool at risk of death. The natural decline rate is the basis for the exponential decay toward zero deaths.
However, as long as the pulse continues, entry of new patients through exposure creates a positive bias for the decay; the decay is an asymptote toward a positive number rather than a decay to zero. As the pulse becomes longer, the system response more closely resembles the step response rather than the impulse response.
In Figure 4, around July 1, 2020 the Illinois curve reached its plateau while the Sweden curve continued to decline. Illinois keeps accumulating deaths and will continue to do so until the pulse stops. The pulse will not stop until there are no more young people to spread virus due to herd immunity. Delay of herd immunity prolongs the plateau of death.
The only way to achieve superior results through government fiat is policy forcing reduced interactions among the elderly or transmission from young to elderly groups. Lockdowns of the young cannot possibly save lives. Texas is an example where policy has been all over the place, but the results are entirely consistent with the expected system response.
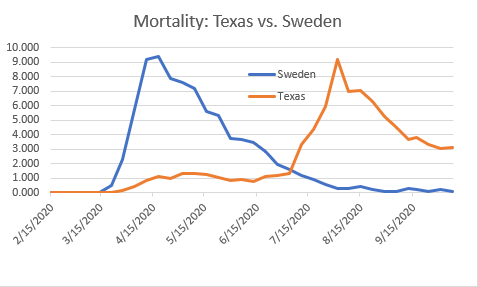
The Texas lockdown began on March 19, 2020. It was sufficiently harsh to have significant effect. The Texas curve had a slower rate of ascent, a delayed local peak (around May 10), and a much lower peak than the Sweden curve. By May 15, the mainstream media was calling the Sweden experiment a failure. Note that by June 3, the Texas curve had reached a plateau.
Phase 3 of reopening in Texas began on June 3. With a short delay consistent with virus incubation and duration of illness, the Texas curve began to climb very quickly. Note that the rate of ascent was lower than Sweden, the time to peak deaths was delayed compared with Sweden, and the peak amplitude was a little lower than Sweden.
However, by August 15, Texas was hitting peak deaths while the pandemic had essentially ended in Sweden. Sweden never closed its schools. Texas had a fierce debate about reopening schools. Sweden never closed its businesses. Many of the businesses in Texas are still closed and will never reopen. Texas is still not open. The Texas curve has not declined to zero but appears to be approaching a significant plateau of around 3 deaths per day per million population. These deaths keep accumulating. On October 10, 2020, Texas mortality (586) passed that of Sweden (583).
What About Denmark?
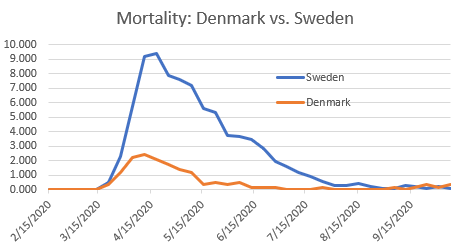
A common response to arguments favorable to laissez-faire is, “What about Denmark?” Figure 6 shows mortality data for Sweden and Denmark. Denmark started a lockdown on March 11, 2020. By early April, Denmark reopened its schools. By early May, Denmark began reopening businesses. The so-called experts scolded Denmark for reopening too soon, but predictions for catastrophe never materialized.
Life is pretty much back to normal in Denmark. Figure 6 demonstrates that the superior results in Denmark cannot be attributed to lockdown of young people. Note that the peak in Denmark mortality occurred sooner than the peak in Sweden. Denmark exposed a smaller group of vulnerable elderly people in a shorter period of time than Sweden.
The superior mortality rate in Denmark indicates that Denmark did a better job than Sweden at protecting its vulnerable elderly people, but there is no evidence that Denmark’s success was due to closing its schools or businesses. If lockdown of the young were responsible for Denmark’s success, then the results of reopening in Denmark would have been the same as the results everywhere else in the world.
Conclusion
To paraphrase Kyle Reese from The Terminator: “Listen. Understand. That virus is out there. It can’t be reasoned with. It can’t be bargained with. It doesn’t feel pity or remorse and it absolutely will not stop. Ever. Until herd immunity is achieved.”
Lockdowns of young people will not work irrespective of how many so-called experts claim otherwise.
What is the best balance between caution and moving forward? Every person has a unique situation. No politician understands your risks and benefits better than you. No central authority has the information necessary for making the best decision for your individual situation. “Listen to the experts. Follow the science.” This is a logical fallacy otherwise known as Appeal to Authority.
An argument or decision stands on its merit rather than the prestige of the person articulating it. The proper role of experts in a free society is to give advice by explaining the options rather than forcing decisions upon free people.










